트리

트리

트리(Tree)비선형적, 계층적, 재귀적 구조를 가진 자료구조이다.(리스트와 스택, 큐는 선형적인 자료구조)
계층적으로 묘사될 수 있는 것은 무엇이든 트리로 나타낼 수 있다.
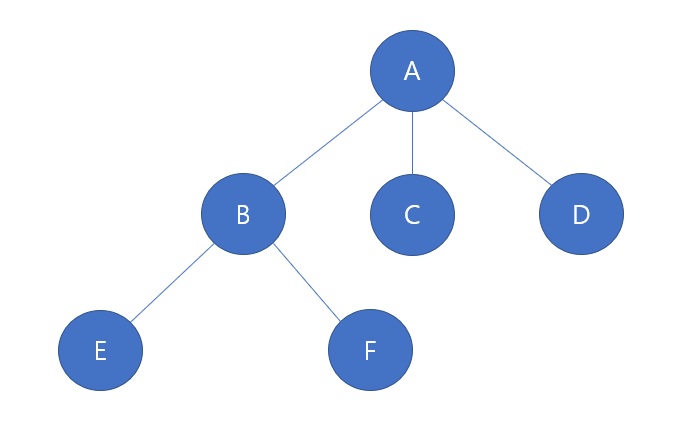트리의 구성요소에 해당하는 A,B,…,F를 노드(Node)라 한다.
B의 바로 아래 있는 E,F를 B의 자식노드(Child Node)라 한다.
반대로 B는 E,F의 부모노드(Parent Node)라 한다.
같은 부모 아래에서 자식노드 서로를 자매노드(Sibling Node)라 부른다. 예를 들어 B,C,D는 서로 자매노드며 E,F도 서로 자매노드이다.
주어진 노드의 상위에 있는 노드들은 조상노드(Ancestor Node)라 한다.
예를 들어 B,A는 F의 조상노드이다.
반대로 어떤 노드의 하위에 있는 노드를 후손노드(Descendant Node)라 한다.
예를 들어 B,E,F,C,D는 A의 후손노드다.

A처럼 부모가 없는 노드, 즉 원조격인 노드를 루트노드(Root Node)라 한다.
반대로 C,D,E,F처럼 자식이 없는 노드를 리프노드(Leaf Node)라 한다.
리프노드를 제외한 모든 노드를 내부노드(Internal Node)라 한다.
둘 이상의 자식노드를 가질 수 있는 트리를 일반트리(General Tree)라 하는 반면에, 최대 두 개까지의 자식노드를 가질 수 있는 트리를 이진트리(Binary Tree)라 한다.

주어진 트리의 부분집합을 이루는 트리를 하위트리(Subtree)라 한다.
위의 그림에서 B,E,F가 하나의 하위트리이며, 또 C 자체로서 하나의 하위트리이다.
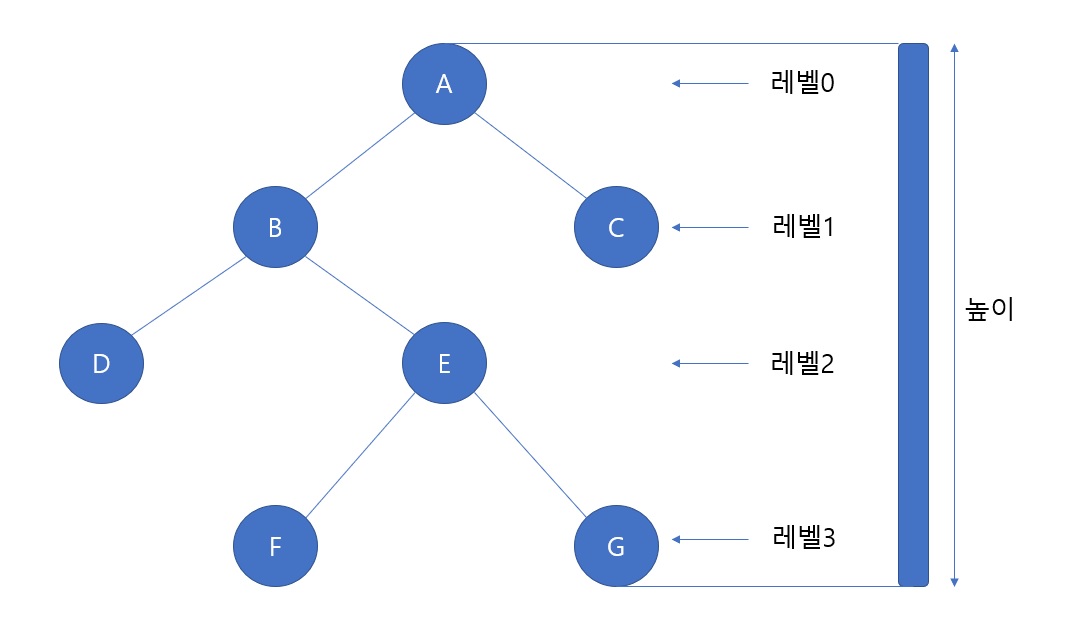트리의 레벨(Level)은 루트노드를 레벨0으로 하고 아래로 내려오면서 증가한다.
트리의 높이(Height)는 트리 내의 최대 레벨과 일치한다.
그림에서 트리의 높이는 3이며 정리하면 트리의 높이는 루트노드로부터 가장 먼 리프노드까지 가는데 필요한 연결(Link)개수를 뜻한다.
즉, 가장 먼 리프노드까지 가기 위해 중간에 지나야 하는 노드 수라고 할 수 있다.
트리의 높이를 공식으로 나타내면 트리의 높이=1+Max(왼쪽 하위트리의 높이, 오른쪽 하위트리의 높이)로 나타낼 수 있다.

트리에서 균형(Balance)을 말할 때가 있다.
여기서 균형이란 루트노드를 기준으로 왼쪽 하위트리와 오른쪽 하위트리 사이의 높이 차이를 말한다.
차이가 1 이하일 때 그 트리를 균형트리(Height Balanced Tree)라 한다.
이에 반해 완전 균형트리(Completely Height Balanced Tree)는 왼쪽, 오른쪽 하위트리 높이가 완전히 일치하는 트리를 말한다.
트리의 균형을 맞춰야하는 이유는 트리에서 데이터에 접근하기 위해 거쳐야하는 노드의 수가 레벨마다 하나인데, 데이터를 찾는데 거쳐야 하는 노드의 수가 적어지기 때문이다.(균형이 차이가 많이 나면 데이터에 접근하기 위해 거쳐야 하는 노드의 수가 매우 많아짐.)