순회

순회

순회(Traversal)란 노드를 삽입, 삭제, 검색하기 위해 트리 내부를 이리저리 돌아다니는 작업을 말한다.
트리 자체가 재귀적으로 정의 되었기 때문에 트리의 순회 역시 재귀적이다.
순회의 종류에는 루트노드에 대한 작업이 어디에 박히느냐에 따라서 전위순회, 중위순회, 후위순회로 나뉘어진다.

전위순회

전위순회(Pre-order Traversal)는 하위트리의 루트노드에 대한 작업이 가장 먼저 일어난다.
전위순회의 전위(Pre-Order)란 말은 해당 노드에 대한 방문 작업이 재귀호출보다 앞서서(전위) 실행된다는 의미이다.

void PreOrder(Nptr T)
{
    if(T!=NULL)
    {
        Visit(T->Name);
        PreOrder(T->LChild);
        PreOrder(T->Rchild);
    }
}

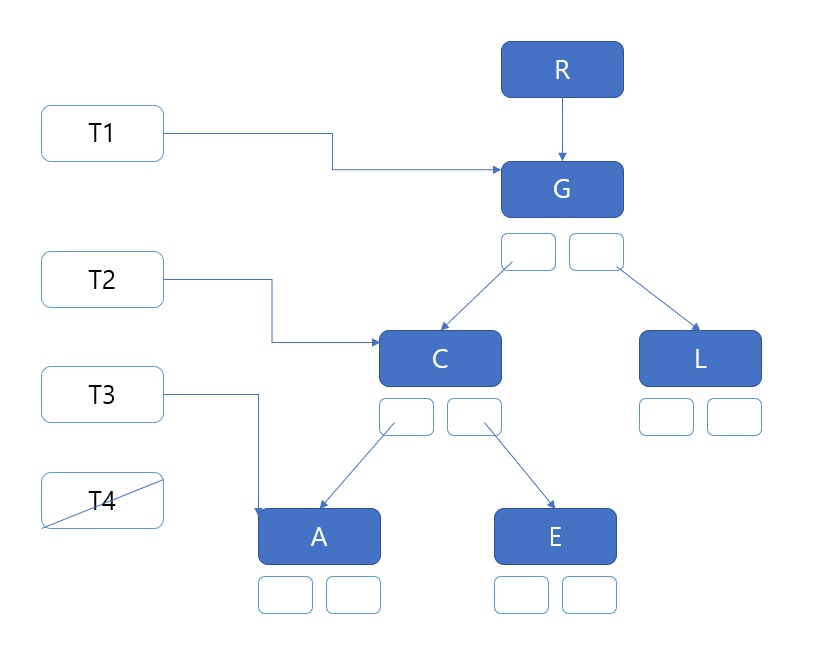
그림에서 트리를 전위순회하면서 노드 데이터를 출력하면 G,C,A,E,L이 된다.
먼저 함수를 호출하는 쪽에서 루트노드 G를 가리키는 포인터 R을 넘기면 이 R이 복사되어 T로 들어간다.
이 T를 T1이라 하면 이제 T1은 노드 G를 가리킨다. 함수가 실행되자마자 데이터 G를 일단 출력하고, G의 LChild를 넘기며 재귀호출한다.
이번에는 G의 LChild가 T로 복사되어 들어간다. 이 T를 T2라 하면 이제 T2는 G의 왼쪽 하위트리를 가리킨다.
C를 루트로 하는 하위트리다. 재귀호출이 시작되자마자 C를 출력하고 C의 LChild가 T3로 복사되어 재귀호출한다.
이런식으로 순회를 반복하면 G,C,A,E,L순으로 출력이 됨을 알 수 있다.

중위순회

중위순회(In-order Traversal)는 Visit작업이 중간에 일어나는 순회를 말한다.

void InOrder(Nptr T)
{
    if(T!=NULL)
    {
        InOrder(T->LChild);
        Visit(T->Name);
        InOrder(T->Rchild);
    }
}

그림에서 트리를 중위순회하면서 노드 데이터를 출력하면 A,C,E,G,L가 된다.

후위순회

후위순회(Post-order Traversal)는 Visit작업이 마지막에 일어나는 순회를 말한다.

void PostOrder(Nptr T)
{
    if(T!=NULL)
    {
        PostOrder(T->LChild);
        PostOrder(T->Rchild);
        Visit(T->Name);
    }
}

그림에서 트리를 후위순회하면서 노드 데이터를 출력하면 A,E,C,L,G가 된다.

레벨순회

전위, 중위, 후위와는 별개로 레벨순회(Level-order Traversal)를 정의하기도 한다.
이 순서는 레벨 0에서 레벨 1로, 다시 레벨 2로 간다.
다시 말해, 트리의 위에서 아래로 진행하되, 같은 레벨에서는 왼쪽에서 오른쪽으로 진행한다.
그림을 레벨순회하면 G,C,L,A,E의 순서로 노드를 방문한다.
레벨순회에 해당하는 재귀호출은 존재하지 않으며 그래프 탐색 방법으로 말하자면 너비우선 탐색에 해당하는 것으로, 큐 구조를 사용하여 구현할 수 있다.