시간복잡도

시간복잡도

시간복잡도 - 단위연산이 수행되는 횟수를 입력 크기에 대한 함수로 구하여 분석
알고리즘을 분석하는 표준
분석 : 모든경우 vs 그렇지 않은 경우
모든 경우 시간복잡도 분석
입력의 크기가 같을 경우, 입력의 값과 상관없이 항상 알고리즘의 성능이 같은 경우
EX )
예: 배열의 수 더하기

• 단위연산: 총합을 계산하기 위한 덧셈
  
• 입력: n, 배열에 있는 항의 개수
  
• T(n) = n
  
  예: 교환정렬
  
• 단위연산: S[j]와 S[i]의 비교
  
• 입력: n, 배열에 있는 항의 개수
  
• T(n) = (n-1)+(n-2)+…+1 = n(n-1)/2
  
  예: 행렬곱셈
  
• 단위연산: 가장 안쪽 for 루프에 있는 곱셈
  
• 입력: 행과 열의 수 -> n
  
• T(n) = n X n X n = n^3
  
  그렇지 않은 경우 시간복잡도
  
• 최악의 경우 시간복잡도
  
• 평균의 경우 시간복잡도
  실제 값이 평균에 크게 벗어나지 않는 경우에만 평균을 “전형적”이다라고 할 수 있음
  EX) 9월 15일의 서울 평균 최고 기온 -> 전형적일 수 있음
  EX) 연평균 소득 -> 전형적이지 않을 수 있음
  
• 최선의 경우 시간복잡도
  
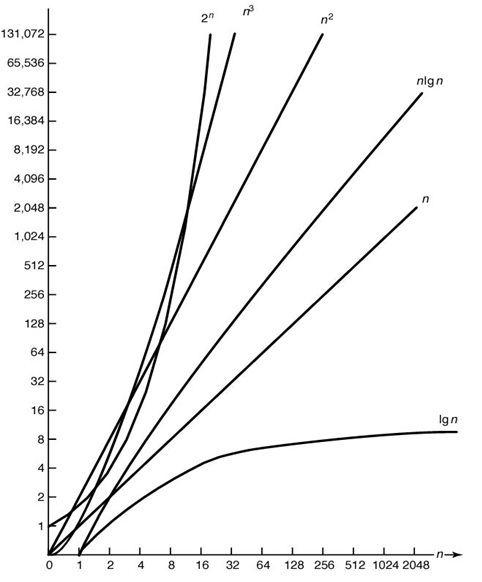
  차수(order)
  알고리즘의 복잡도를 표시하기 위하여 사용하는 표기법
  시간복잡도가 2차인 알고리즘은 입력 크기가 충분히 크면 각 알고리즘에서 단위연산의 수행시간과 무관하게 시간복잡도가 n인 것보다 우수할 수 없다.
  
  시간복잡도
  
  빅오
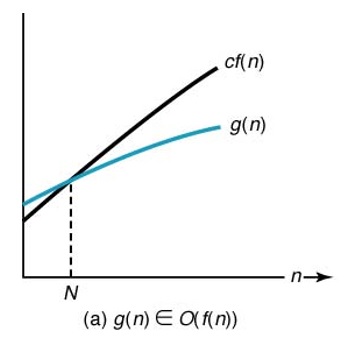  정의 : 주어진 복잡도 함수 f(n)에 대하여, O(f(n))은 n ≥ N을 만족하는 모든 n에 대하여 부등식 g(n) ≤ c × f (n) 을 만족하는 양의 실수 c와 음이 아닌 정수 N이 존재하는 복잡도 함수 g(n)의 집합이다.
  결론적으로 해당 알고리즘은 big O보다 더 오래걸릴 수 없다는 최악의 경우의 알고리즘이다.
  현실에서는 항상 최악의 경우를 생각해야 하기 때문에, 흔히 빅오 표기법을 많이 사용한다.
  
  빅오메가
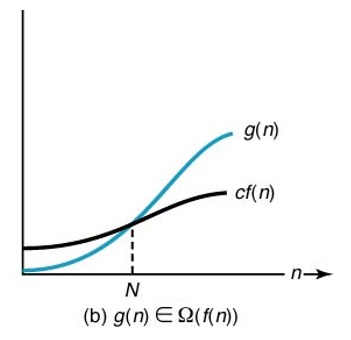  정의 : 주어진 복잡도 함수 f(n)에 대하여, (f(n))은 n ≥ N을 만족하는 모든 n에 대해 부등식을 g(n) ≥ c × f (n) 을 만족하는 양의 실수 c와 음이 아닌 정수 N이 존재하는 복잡도 함수 g(n)의 집합이다.
  결론적으로 해당 알고리즘은 빅오메가보다 더 빠를 수 없다는 최선의 경우의 알고리즘이다.
  
  빅세타
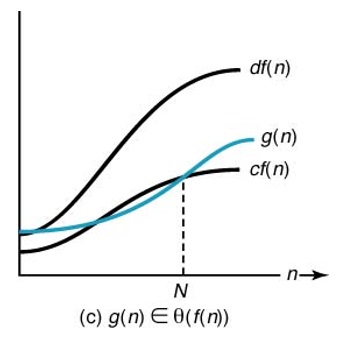  빅오와 빅오메가를 하나로 합쳐 표현한 평균적인 경우의 알고리즘이다.